Analysis of Step 2

The second step concerns the 3-D, non-reacting cold flow, used as validation by comparison with the published results of a pseudo-spectral solver . The main quantities of interest for this comparison are:

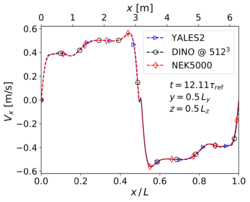
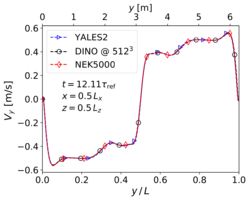
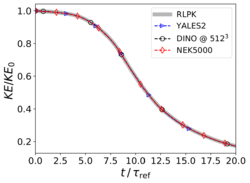
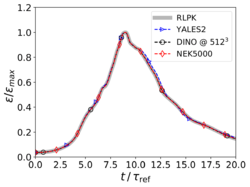
1. Velocity profiles along centerlines of the domain at $t=12.11\tau _{ref}$, as illustrated in Fig. 5. 2. The evolution of kinetic energy ($k(t)={\frac {1}{2}}<u_{i}u_{i}>$) and of its dissipation rate ($\epsilon (t)=dk/dt=2\nu <S_{ij}S_{ij}>$) versus time, as shown in Fig. 6, where $S_{ij}$ is the symmetric strain-rate tensor,

$S_{ij}={\frac {1}{2}}({\frac {\partial u_{i}}{\partial x_{j}}}+{\frac {\delta u_{j}}{\delta x_{i}}})$ ; (11)

Comparing the velocity fields at $t=12.11\tau _{ref}$ is done on purpose. As known from the TGV literature, this instant corresponds to a complex pseudo-turbulent field, before further turbulence decay due to dissipation (see also Figure 9 in ). Getting the correct velocity field in these conditions is challenging, since the obtained results are very sensitive with regard to the employed algorithms and discretization. Unlike the 2-D situation, no analytical solution is available there, and the results can only be compared to other numerical simulations. In the present case, the reference data are taken from a simulation relying on the pseudo-spectral code RLPK using $512^{3}$ grid points .

Velocities along the centerlines of the domain for cold 3-D TGV case (Step 2) at $t=12.11\tau _{ref}$.

First, it appears on Fig. 5 that no differences can be identified visually from the velocity fields along the centerlines at $t=12.11\tau _{ref}$. Looking at Figs. 6 it can be observed that the three codes are able to reproduce the evolution of turbulence kinetic energy without any visible differences, whereas for the dissipation rate minute deviations appear at two instants (see enlargements in Fig. 6, right): (1) shortly after transition ($11<t/\tau _{ref}<13.5$) for YALES2, and (2) just before flow relaminarization ($16.25<t/\tau _{ref}20$) for both DINO and YALES2. The results of RLPK and of Nek5000 coincide visually at all times. These two time-instants are very sensitive moments at which the accuracy of the numerical methods and the resolution in time and space appear to play a major role. These small discrepancies are regarded as minor and considered acceptable with respect to the validation process of the codes. It must also be kept in mind that the data used as a reference have been obtained with a resolution of $512^{3}$ grid points with a pseudo-spectral solver.

Here is the evolution with time of turbulent kinetic energy k (left, written KE in vertical axis) and of its dissipation rate $\epsilon$ (right), by comparison with published reference data from .