Difference between revisions of "Analysis of Step 3"
| (5 intermediate revisions by the same user not shown) | |||
| Line 10: | Line 10: | ||
The results that will be compared involve: | The results that will be compared involve: | ||
| − | 1. '''Velocity profiles''' at <math>t = 2 \tau_{ref} = 0.5 ms</math> along the centerlines of the domain | + | 1. '''Velocity profiles''' at <math>t = 2 \tau_{ref} = 0.5 ms</math> along the centerlines of the domain; |
| − | 2. Profiles of <math>H_2</math> and <math>O_2</math> '''mass fractions''' and '''profile of temperature''' at <math>t = 2 \tau_{ref} = 0.5 ms</math> along the y-centerline of | + | 2. '''Profiles''' of <math>H_2</math> and <math>O_2</math> '''mass fractions''' and '''profile of temperature''' at <math>t = 2 \tau_{ref} = 0.5 ms</math> along the y-centerline of |
| − | the domain | + | the domain; |
| − | 3. '''Evolution of maximal temperature''' in the domain vs. time | + | 3. '''Evolution of maximal temperature''' in the domain vs. '''time'''. |
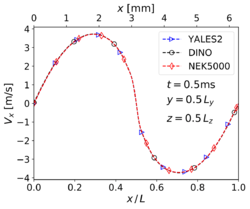
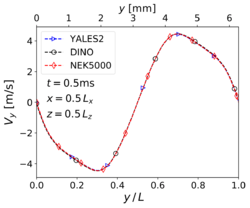
| − | Looking at the results of '''velocity''' | + | Looking at the results of '''velocity''' at time <math>t = 2 \tau_{ref} = 0.5 ms</math> along the centerlines of the computational domain, |
it is observed that the three codes deliver the same '''velocity profiles'''; the agreement is visually perfect. | it is observed that the three codes deliver the same '''velocity profiles'''; the agreement is visually perfect. | ||
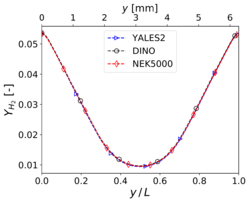
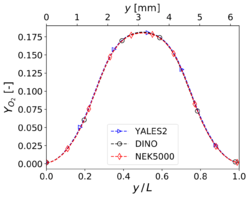
The results for the two main species '''mass fractions''' (<math>Y_{H2}</math> | The results for the two main species '''mass fractions''' (<math>Y_{H2}</math> | ||
and <math>Y_{O2}</math>) are also in excellent agreement among the | and <math>Y_{O2}</math>) are also in excellent agreement among the | ||
| − | three participating codes | + | three participating codes. |
| − | [[File:vx_x_3d_nonreacting. | + | [[File:vx_x_3d_nonreacting.png|250px]] |
| − | [[File:vy_y_3d_nonreacting. | + | [[File:vy_y_3d_nonreacting.png|250px]] |
| − | [[File:yh2_y_nonreacting. | + | [[File:yh2_y_nonreacting.png|250px]] |
| − | [[File:yo2_y_nonreacting. | + | [[File:yo2_y_nonreacting.png|250px]] |
| − | Profile of mass fractions of <math>H_2</math> (left) and <math>O_2</math> (right) at <math>t = 2 \tau_{ref} ms</math>, <math>x = 0.5L</math>, and <math>z = 0.5L</math> for '''3-D non-reacting multi-species flow''' ('''Step 3'''). | + | '''Profile of mass fractions''' of <math>H_2</math> (left) and <math>O_2</math> (right) at <math>t = 2 \tau_{ref} ms</math>, <math>x = 0.5L</math>, and <math>z = 0.5L</math> for '''3-D non-reacting multi-species flow''' ('''Step 3'''). |
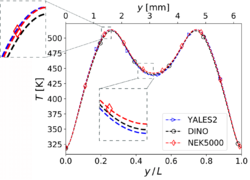
| − | Regarding temperature, | + | [[File:T_y_nonreacting_withzoom.png|250px]] |
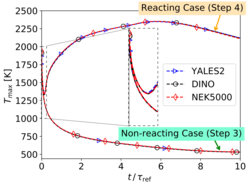
| − | deviations are revealed in the inlaid enlargements shown in | + | [[File:tmax_nonreacting_3d_withzoom.png|250px]] |
| − | Finally, the evolution with time of maximum temperature inside the computational domain is presented in | + | |
| + | Regarding temperature, the figure on the left shows along the centerline '''two peaks''' and '''one valley''', as expected. Very small | ||
| + | deviations are revealed in the inlaid enlargements shown in this figure. | ||
| + | Finally, the evolution with time of maximum temperature inside the computational domain is presented in the figure on the right. | ||
Here again, no differences are observed at all concerning this parameter. | Here again, no differences are observed at all concerning this parameter. | ||
As a conclusion concerning this step, the three codes are able to reproduce numerically the behavior of a complex multi-species, non-isothermal flow with excellent agreement, and are thus strong candidates for high-fidelity | As a conclusion concerning this step, the three codes are able to reproduce numerically the behavior of a complex multi-species, non-isothermal flow with excellent agreement, and are thus strong candidates for high-fidelity | ||
simulations of turbulent flames, as considered in the next and final step. | simulations of turbulent flames, as considered in the next and final step. | ||
Latest revision as of 04:47, 26 August 2020
The main difference between this step and the previous one, is that now species and heat diffusion are additionally taken into account in an inhomogeneous environment. Neither analytical nor reference solution are available for this configuration, so that only comparisons between the three codes involved in the benchmark are possible. Compared to Step 2, the presence of high-temperature regions additionally modifies the evolution of the TGV with time, turbulence being locally damped due to dilatation and higher viscosities. As a consequence, the needed resolution for this case is less than in Step 2: YALES2 and DINO used only 256 grid points in each direction while Nek5000 used 36 elements (again with 7 Gauss-Lobatto-Legendre points in each element), i.e. 252 points in each direction.
The results that will be compared involve:
1. Velocity profiles at along the centerlines of the domain;
2. Profiles of and mass fractions and profile of temperature at along the y-centerline of the domain;
3. Evolution of maximal temperature in the domain vs. time.
Looking at the results of velocity at time along the centerlines of the computational domain, it is observed that the three codes deliver the same velocity profiles; the agreement is visually perfect. The results for the two main species mass fractions ( and ) are also in excellent agreement among the three participating codes.
Profile of mass fractions of (left) and (right) at , , and for 3-D non-reacting multi-species flow (Step 3).
Regarding temperature, the figure on the left shows along the centerline two peaks and one valley, as expected. Very small deviations are revealed in the inlaid enlargements shown in this figure. Finally, the evolution with time of maximum temperature inside the computational domain is presented in the figure on the right. Here again, no differences are observed at all concerning this parameter. As a conclusion concerning this step, the three codes are able to reproduce numerically the behavior of a complex multi-species, non-isothermal flow with excellent agreement, and are thus strong candidates for high-fidelity simulations of turbulent flames, as considered in the next and final step.