Difference between revisions of "Step 2"
(→Step 2 Description) |
(→Step 2 Description) |
||
| (9 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
The next step in the benchmark is to simulate the '''Taylor-Green Vortex configuration in 3-D''', still for a '''single-component incompressible flow'''. | The next step in the benchmark is to simulate the '''Taylor-Green Vortex configuration in 3-D''', still for a '''single-component incompressible flow'''. | ||
| − | For this configuration, a reference solution obtained with a pseudo-spectral solver is available in the scientific literature<ref name="vanrees2011" | + | For this configuration, a reference solution obtained with a pseudo-spectral solver is available in the scientific literature<ref name="vanrees2011"/> and can be used for validation by a direct comparison. |
The domain size has been set to <math>L = 2 \pi L_0</math> in each direction, where <math>L_0 = 1\; \mathrm{m}</math> is an arbitrarily-chosen reference length scale for dimensional codes. As in the previous section, periodic boundary conditions are used in all three spatial directions. | The domain size has been set to <math>L = 2 \pi L_0</math> in each direction, where <math>L_0 = 1\; \mathrm{m}</math> is an arbitrarily-chosen reference length scale for dimensional codes. As in the previous section, periodic boundary conditions are used in all three spatial directions. | ||
| Line 8: | Line 8: | ||
The initial conditions for 3-D TGV are given by the following set of equations: | The initial conditions for 3-D TGV are given by the following set of equations: | ||
| − | <math>u(x,y,z,0) = +u_0 \times sin(x/L_0) \times cos(y/L_0) \times cos(z/L_0)</math> | + | '''(Eq. 1)''' <math>u(x,y,z,0) = +u_0 \times \sin(x/L_0) \times \cos(y/L_0) \times \cos(z/L_0)</math> |
| − | <math>v(x,y,z,0) = -u_0 \times \cos(x/L_0) \times \sin(y/L_0) \times \cos(z/L_0)</math> | + | '''(Eq. 2)''' <math>v(x,y,z,0) = -u_0 \times \cos(x/L_0) \times \sin(y/L_0) \times \cos(z/L_0)</math> |
| − | <math> w(x,y,z,0) = 0 </math> | + | '''(Eq. 3)''' <math> w(x,y,z,0) = 0</math> |
The reference velocity magnitude is set again to <math>u_0 = 1 \; \mathrm{m/s}</math>. | The reference velocity magnitude is set again to <math>u_0 = 1 \; \mathrm{m/s}</math>. | ||
| Line 26: | Line 26: | ||
This values are actually quite conservative since the focus of this study is set on accuracy comparisons and not on pure computational performance. | This values are actually quite conservative since the focus of this study is set on accuracy comparisons and not on pure computational performance. | ||
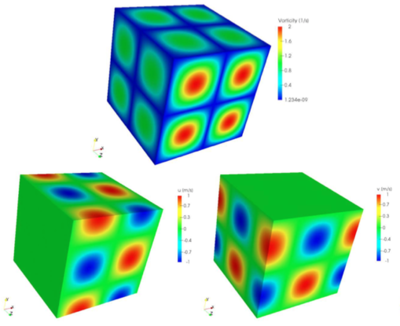
| − | ''' | + | The image below gives an indication of the initial fields of the velocity components and of the vorticity obtained thanks to the '''(Eq. 1)''', '''(Eq. 2)''' and '''(Eq. 3)'''. |
| − | + | ||
| − | + | [[File:fields_step2.png|400px|fields step 2]] | |
| − | |||
| − | |||
| − | |||
| − | + | The evolution of the magnitude of the velocity and of the vorticity are presented on the following video: | |
<div class="infobox" style="width: 700px;"> | <div class="infobox" style="width: 700px;"> | ||
| − | {| class="floatright" style="border: 1px solid #ccc; margin: | + | {| class="floatright" style="border: 1px solid #ccc; margin: 50px;" |
|{{#widget:YouTube|id=k7JRrvBOSSY|width=600|height=500}} | |{{#widget:YouTube|id=k7JRrvBOSSY|width=600|height=500}} | ||
|} | |} | ||
| Line 51: | Line 47: | ||
= References = | = References = | ||
| − | + | <references> | |
| − | + | <ref name="vanrees2011"> | |
| − | + | <bibtex> | |
| − | + | @article{Vanrees2011, | |
| + | author= {W.M. van Rees, A. Leonard, D.I. Pullin, and P. Koumoutsakos}, | ||
| + | title= {A comparison of vortex and pseudo-spectral | ||
| + | methods for the simulation of periodic vortical flows at high Reynolds numbers.}, | ||
| + | journal={J. Comput. Phys.}, | ||
| + | year= {2011}, | ||
| + | volume={230}, | ||
| + | pages={2794--2805}, | ||
| + | } | ||
| + | </bibtex> | ||
| + | </ref> | ||
| + | </references> | ||
Latest revision as of 21:40, 24 August 2020
Step 2 Description
The next step in the benchmark is to simulate the Taylor-Green Vortex configuration in 3-D, still for a single-component incompressible flow. For this configuration, a reference solution obtained with a pseudo-spectral solver is available in the scientific literature[1] and can be used for validation by a direct comparison.
The domain size has been set to in each direction, where is an arbitrarily-chosen reference length scale for dimensional codes. As in the previous section, periodic boundary conditions are used in all three spatial directions.
The initial conditions for 3-D TGV are given by the following set of equations:
(Eq. 1)
(Eq. 2)
(Eq. 3)
The reference velocity magnitude is set again to . The desired Reynolds number is again , as in the previous section, since this value has been used as well in the reference study employed for comparison[1]. To obtain the proper value of Re, the kinematic viscosity is set once again to . With this set of parameters, the reference time scale is . The flow simulation must be carried out for a physical time of .
Regarding spatial discretization, a resolution of at least 512 nodes (or cells) in each direction is recommended. This value leads to an over-resolved simulation during the first few but is necessary to capture properly the transition to turbulence that should occur between 10 and 15 . As a point of comparison, the reference solution from[1] has been obtained with a spectral code on a grid. The timestep should be chosen to ensure that the maximum values of the Courant-Friedrichs-Lewy (CFL) and Fourier (Fo) numbers remain below and , respectively. This values are actually quite conservative since the focus of this study is set on accuracy comparisons and not on pure computational performance.
The image below gives an indication of the initial fields of the velocity components and of the vorticity obtained thanks to the (Eq. 1), (Eq. 2) and (Eq. 3).
The evolution of the magnitude of the velocity and of the vorticity are presented on the following video:
Aside Suggestion
Check mesh convergence and time integration independence.
Check that
References
- ↑ 1.0 1.1 1.2
W.M. van Rees, A. Leonard, D.I. Pullin,, P. Koumoutsakos, A comparison of vortex and pseudo-spectral
methods for the simulation of periodic vortical flows at high Reynolds numbers., J. Comput. Phys. 230:2794--2805, 2011, BibtexAuthor : W.M. van Rees, A. Leonard, D.I. Pullin,, P. Koumoutsakos
Title : A comparison of vortex and pseudo-spectral methods for the simulation of periodic vortical flows at high Reynolds numbers.
In : J. Comput. Phys. -
Address :
Date : 2011