Difference between revisions of "Step 1"
(→Step 1 Description) |
(→References) |
||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
= Step 1 Description = | = Step 1 Description = | ||
| − | The 2-D TGV test case has been already well documented in the scientific literature, e.g. <ref name="abelsamie2016" /><ref name="Laizet2009"/>. | + | The '''2-D TGV''' test case has been already well documented in the scientific literature, e.g. <ref name="abelsamie2016"/><ref name="Laizet2009"/>. |
Therefore, only a brief description is given here. | Therefore, only a brief description is given here. | ||
| − | This configuration is used as verification step, since an analytic solution exists | + | This configuration is used as verification step, since an analytic solution exists<ref name="Taylor1937"/>. |
| − | An incompressible flow with constant density and viscosity is simulated. | + | An '''incompressible flow''' with constant density and viscosity is simulated. |
The fluid is contained in a square box of dimension <math>[0;L]^2</math> with periodic boundary conditions in both directions. | The fluid is contained in a square box of dimension <math>[0;L]^2</math> with periodic boundary conditions in both directions. | ||
| Line 21: | Line 21: | ||
with <math>u_0 = 1 \; \mathrm{m/s}</math>. | with <math>u_0 = 1 \; \mathrm{m/s}</math>. | ||
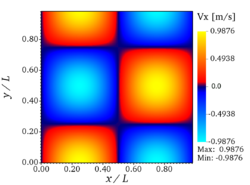
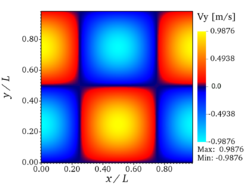
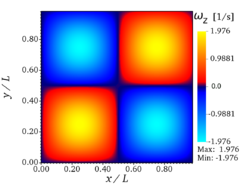
| − | The flow is thus initially composed of four vortices, one in each quarter of the box. | + | |
| − | The vortex turnover time is defined as <math>\tau_\mathrm{ref} = L_0/u_0 = 1\;\mathrm{s}</math>. | + | The flow is thus initially composed of '''four vortices''', one in each quarter of the box. |
| + | The vortex '''turnover time''' is defined as <math>\tau_\mathrm{ref} = L_0/u_0 = 1\;\mathrm{s}</math>. | ||
For non-dimensional codes, the relevant parameter for this simulation is the vortex Reynolds number, <math>Re=u_0 L_0/\nu = 1,600</math> in the present setup. | For non-dimensional codes, the relevant parameter for this simulation is the vortex Reynolds number, <math>Re=u_0 L_0/\nu = 1,600</math> in the present setup. | ||
It should be noted that the theoretical solution is only stable for sufficiently small Reynolds numbers, explaining why the particular value <math>Re=1,600</math> has been chosen here, as done in many previous studies using the TGV configuration. | It should be noted that the theoretical solution is only stable for sufficiently small Reynolds numbers, explaining why the particular value <math>Re=1,600</math> has been chosen here, as done in many previous studies using the TGV configuration. | ||
| − | A major interest of this test-case is that an analytical solution has been derived for such conditions | + | A major interest of this test-case is that an analytical solution has been derived for such conditions<ref name="Taylor1937"/>: |
<math> | <math> | ||
| Line 35: | Line 36: | ||
v(x,y,t) = v(x,y,0) \times \mathrm{e}^{-2\nu t/L_0^2} = v(x,y,0) \times \mathrm{e}^{-2 \, (t/\tau_{\mathrm{ref}}) / \mathrm{Re}} \,. | v(x,y,t) = v(x,y,0) \times \mathrm{e}^{-2\nu t/L_0^2} = v(x,y,0) \times \mathrm{e}^{-2 \, (t/\tau_{\mathrm{ref}}) / \mathrm{Re}} \,. | ||
</math> | </math> | ||
| + | |||
| + | [[File:vx_t2.png|250px|alt text]] | ||
| + | [[File:vy_t2.png|250px|alt text]] | ||
| + | [[File:wz_t2.png|250px|alt text]] | ||
| + | |||
All physical conditions are now completely defined and only numerical parameters remain to be set. | All physical conditions are now completely defined and only numerical parameters remain to be set. | ||
| Line 42: | Line 48: | ||
= Aside suggestions = | = Aside suggestions = | ||
| − | = | + | This step should clearly not be a big issue for any code. |
| + | However, it is a good way to verify the orders of '''convergence''' (both in space and time), to check any '''stability issues''', to measure the influence of the convergence criteria of iterative solvers (if any), etc... | ||
| + | |||
| + | = References = | ||
| + | |||
<references> | <references> | ||
| − | <ref name="abelsamie2016">A. Abdelsamie and G. Fru and F. Dietzsch and G. Janiga and D. Thévenin , | + | <ref name="abelsamie2016"> |
| − | <ref name="Laizet2009">S. Laizet and E. Lamballais , | + | <bibtex> |
| + | @article{Abdelsamie2016, | ||
| + | author= {A. Abdelsamie and G. Fru and F. Dietzsch and G. Janiga and D. Thévenin}, | ||
| + | title= {Towards direct numerical simulations of low-Mach number turbulent reacting and two-phase flows using immersed boundaries}, | ||
| + | journal={Comput. Fluids}, | ||
| + | year= {2016}, | ||
| + | volume={131}, | ||
| + | number={5}, | ||
| + | pages={123--141}, | ||
| + | } | ||
| + | </bibtex> | ||
| + | </ref> | ||
| + | <ref name="Laizet2009"> | ||
| + | <bibtex> | ||
| + | @article{Laizet2009, | ||
| + | author= {S. Laizet and E. Lamballais}, | ||
| + | title= {High-order compact schemes for incompressible flows: A simple and efficient method with quasi-spectral accuracy}, | ||
| + | journal={J. Comput. Phys.}, | ||
| + | year= {2009}, | ||
| + | volume={228}, | ||
| + | pages={5989--6015}, | ||
| + | } | ||
| + | </bibtex> | ||
| + | </ref> | ||
| + | <ref name="Taylor1937"> | ||
| + | <bibtex> | ||
| + | @article{Taylor1937, | ||
| + | author= {G.I. Taylor and A.E. Green}, | ||
| + | title= {Mechanism of the production of small eddies from large ones}, | ||
| + | journal={Proc. Royal Soc. A}, | ||
| + | year= {1937}, | ||
| + | volume={158}, | ||
| + | issue={895}, | ||
| + | pages={499--521}, | ||
| + | } | ||
| + | </bibtex> | ||
| + | </ref> | ||
</references> | </references> | ||
Latest revision as of 14:41, 25 August 2020
Step 1 Description
The 2-D TGV test case has been already well documented in the scientific literature, e.g. [1][2]. Therefore, only a brief description is given here. This configuration is used as verification step, since an analytic solution exists[3].
An incompressible flow with constant density and viscosity is simulated.
The fluid is contained in a square box of dimension with periodic boundary conditions in both directions. The value with has been arbitrarily chosen in the present benchmark for dimensional codes. The numerical value for the kinematic viscosity is chosen as to get suitable conditions, as discussed below. The initial velocity components are prescribed as follows:
with .
The flow is thus initially composed of four vortices, one in each quarter of the box. The vortex turnover time is defined as . For non-dimensional codes, the relevant parameter for this simulation is the vortex Reynolds number, in the present setup. It should be noted that the theoretical solution is only stable for sufficiently small Reynolds numbers, explaining why the particular value has been chosen here, as done in many previous studies using the TGV configuration.
A major interest of this test-case is that an analytical solution has been derived for such conditions[3]:
All physical conditions are now completely defined and only numerical parameters remain to be set.
Based on previously published studies, the recommended parameters for time and space discretization are and grid points in each direction.
The flow must be simulated for a physical time of .
Aside suggestions
This step should clearly not be a big issue for any code. However, it is a good way to verify the orders of convergence (both in space and time), to check any stability issues, to measure the influence of the convergence criteria of iterative solvers (if any), etc...
References
- ↑
A. Abdelsamie, G. Fru, F. Dietzsch, G. Janiga, D. Thévenin, Towards direct numerical simulations of low-Mach number turbulent reacting and two-phase flows using immersed boundaries, Comput. Fluids 131(5):123--141, 2016, BibtexAuthor : A. Abdelsamie, G. Fru, F. Dietzsch, G. Janiga, D. Thévenin
Title : Towards direct numerical simulations of low-Mach number turbulent reacting and two-phase flows using immersed boundaries
In : Comput. Fluids -
Address :
Date : 2016 - ↑
S. Laizet, E. Lamballais, High-order compact schemes for incompressible flows: A simple and efficient method with quasi-spectral accuracy, J. Comput. Phys. 228:5989--6015, 2009, BibtexAuthor : S. Laizet, E. Lamballais
Title : High-order compact schemes for incompressible flows: A simple and efficient method with quasi-spectral accuracy
In : J. Comput. Phys. -
Address :
Date : 2009 - ↑ 3.0 3.1
G.I. Taylor, A.E. Green, Mechanism of the production of small eddies from large ones, Proc. Royal Soc. A 158:499--521, 1937, BibtexAuthor : G.I. Taylor, A.E. Green
Title : Mechanism of the production of small eddies from large ones
In : Proc. Royal Soc. A -
Address :
Date : 1937